Video: Free particle I
Slides
In this chapter we will investigate the simplest possible scenario one can consider in the context of mechanics — a free particle — one with no forces acting upon it whatsoever. We will see that, given everything we have learnt up until this point, that we can directly solve for the evolution of a free particle, since we can immediately find the the energy eigenstates (the quantum states of a particle with a definite energy) in this simple setting.
We will see that quantum evolution is more intricate than classical evolution, ultimately due to the HUP. In particular, in a classical setting, if a particle has an initial position and an initial momentum , then from the equation of motion — Newton’s second law — the position of the particle at time will be
(and the momentum is constant, ).
In quantum mechanics, as we already saw, a particle must necessarily have a superposition of momenta. This means that it will be travelling with a superposition of speeds, and therefore after some time, it will be in a superposition of having different displacements from its initial position (i.e. of having travelled different distances). As we will see, this generically leads to spreading out of the wavefunction, so that at later times, a position measurement will generally have a larger standard deviation.
6.1States of definite energy¶
Our starting point, as will always be the case, is to ask the question what are the energy eigenstates of a free particle?, that is, what are the states of definite energy? While in general this is a subtle question, when there are no forces acting on the particle, the situation is much simpler. This is because in this case, no forces translates into a vanishing potential energy , and hence the Hamiltonian becomes simply
i.e. the total energy of the particle is just the kinetic energy. When will a particle have a definite kinetic energy? This is easy to answer: it will have a definite kinetic energy when it has a definite momentum. This therefore suggests that for a free particle
For a free particle, momentum eigenstates are energy eigenstates.
We can directly verify that this is the case, and find the corresponding energy eigenvalue:
where to arrive at the second line we used the fact that , i.e. is an eigenstate of with eigenvalue .
What (6.3) shows is that is an eigenstate of (i.e. an energy eigenstate) with energy . This is exactly as it should be, since if a particle has a definite momentum , then it has a (definite) kinetic energy .
There are two important points to note at this stage. First, there are in fact two states each with the same energy: the state and both have energy . This is intutive, since the kinetic energy doesn’t care about the velocity but only the speed of the particle, and is hence insensitive to the sign of the momentum. This means that there are two energy eigenstates for every energy eigenvalue. This is known as degeneracy and we will study this further once we move into 3D at the end of this unit. Because of this degeneracy in energy, it will be essential to keep track of the momentum, and hence we will work with momentum eigenstates (and momentum wavefunctions), rather than energy eigenstates.
Second, since momentum is continuous we see that for a free particle, energy is always continuous. This is consistent with what we saw in the previous chapter: there we learnt that the energy will be continuous when the particle isn’t bound to a potential well. Since there is no potential well for a free particle, the particle is most certainly not bound, and hence we have a continuous range of energies, as expected.
6.2Time evolution of a free particle I¶
Given the above, it is now straightforward to write down the time evolution of a free particle in quantum mechanics. As in the previous chapter, we will begin by expressing the initial state in terms of the energy eigenstates for a free particle, i.e. given the discussion above, of momentum eigenstates. We can realise that this is exactly as we did previously in Chapter 2: The momentum of a quantum particle, in terms of the momentum wavefunction. In particular, what we called in the previous chapter, we will call here , since (5.6) becomes
where we add the subscript to the momentum wavefunction to denote the fact that this is the initially specified momentum wavefunction. We can now use the superposition principle (i.e. (5.12)) to write down the state at time . In particular, since is an energy eigenstate with energy , it will evolve into , at time , and hence the superposition (6.4) will evolve into
which is readily seen to satisfy the initial condition .
It is insightful to express this in a slightly different way, solely in terms of momentum wavefunctions. What (6.5) shows is that if we know that the momentum wavefunction at is
then it will evolve into the wavefunction given by
This equation restates what we already knew, but makes it much clearer. In particular, it says that for a free particle, if we specify the state in terms of the momentum wavefunction, then the evolution is remarkably simple: the wavefunction just acquires a phase in time! This is because momentum eigenstates are states of definite energy — and are thus stationary states.
6.3Time evolution of a free particle II¶
Video: Free particle II
Slides
Equations (6.5) and (6.7) in principle give a complete solution to the evolution of a free quantum particle. Hence, in principle, we could end the chapter here (after an example maybe). However, this isn’t a particularly useful place to stop. The reason for this is that usually we are interested in the spatial wavefunction and its evolution in time. What we would really like to be able to do therefore is to specify an initial spatial wavefunction , and find the wavefunction that it evolves into. We will do this in this section.
We already have all the ingredients we need, we just need to put them all together. First, if the initial condition is specified by a spatial wavefunction , then in order to use (6.7) we need to recall how to express in terms of it. This is through the (inverse) Fourier transform, (2.20). That is,
Substituting this into (6.7), we have thus half-solved our problem:
since this now gives a momentum wavefunction at time in terms of a spatial initial wavefunction. We can finish off our goal, by performing a second Fourier transform (now using (2.19)), transforming the momentum wavefunction into a spatial wavefunction . The one subtlety that we need to take care with is that we already used as our (dummy) integration variable, but we now want to use instead as the position variable in . We therefore need to change our integration variable to for consistency. Altogether, after some simple re-arranging and simplifying, we obtain
This is a formidible looking expression, involving a double integration! From this perspective, quantum evolution looks highly complicated. However, this is completely equivalent to (6.7). This highlights an important lesson: just because something appears complicated, doesn’t mean it doesn’t have a simpler form. Equation (6.10) is useful as it shows how a spatial wavefunction at time depends upon the spatial wavefunction at time , however if we only had this we wouldn’t really understand anything. In contrast, we do know how to understand this equation: it is the combination of the relationship between spatial and momentum wavefunctions, combined with the simple evolution of momentum wavefunctions.
In general it isn’t possible to simplify or evaluate anayltically the right-hand side of (6.10). That is, if you want to consider a generic initial wavefunction , and ask how it evolves in time, then it isn’t possible to write down a closed form expression (one not involving integral(s)) for the wavefunction at time . Does this mean that (6.10) is useless? The answer is absolutely not. Even though we can’t get a closed form expression, it is very easy to numerically integrate the right-hand side, and thus study the evolution numerically.
6.4Gaussian wavefunction¶
There is one special initial wavefunction whose evolution can be solved analytically. This is the Gaussian wavefunction which we will now study.
Consider that the wavefunction of a particle is initially given by
where and are constants. This is closely related to the wavefunction we encountered in (3.1), except for the additional phase factor . As you will show in an exercise, this has the effect of increasing the average momentum of the particle by . Hence, we are now considering a moving particle instead of a stationary one, which initially has a spread .
Substituting this into (6.10), after a lengthy and fiddly calculation, it is possible to solve analytically for . We find
where is a time-dependent phase factor (which we won’t actually write down, as its form isn’t too important), and where
This wavefunction is remarkably similar in form to (6.11), except for a couple of key differences:
The gaussian becomes centred at at time . That is, the gaussian is moving with constant velocity . This is similar to a classical free particle which moves with constant velocity!
The width of the gaussian changes in time. Recall that standard deviation of the position of the particle was initially given by . Given the form of the wavefunction (6.12), we can read off that
This grows in time, from the initial value . It is important to note that is independent of , i.e. independent of how fast the particle is moving. This is thus a univerisal feature of the dynamics of the wavefunction. We will return to this below.
Finally, there is a phase factor . This term is complicated, but it accounts for correlations which build up, between where the particle is and what momentum it has.
It is insightful to plot the wavefunction as it evolves in time. We do this below, both for the wavefunction and the associated probability density , both as an animation and in stills:
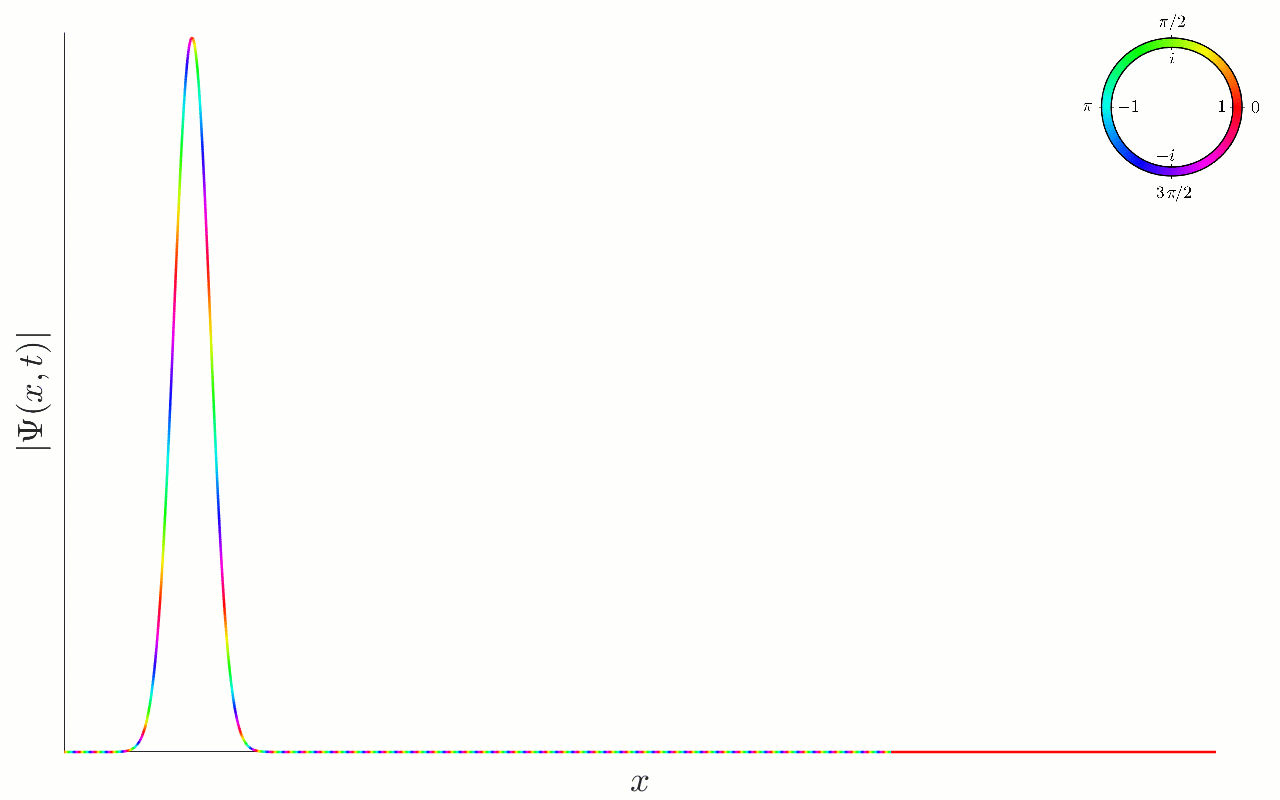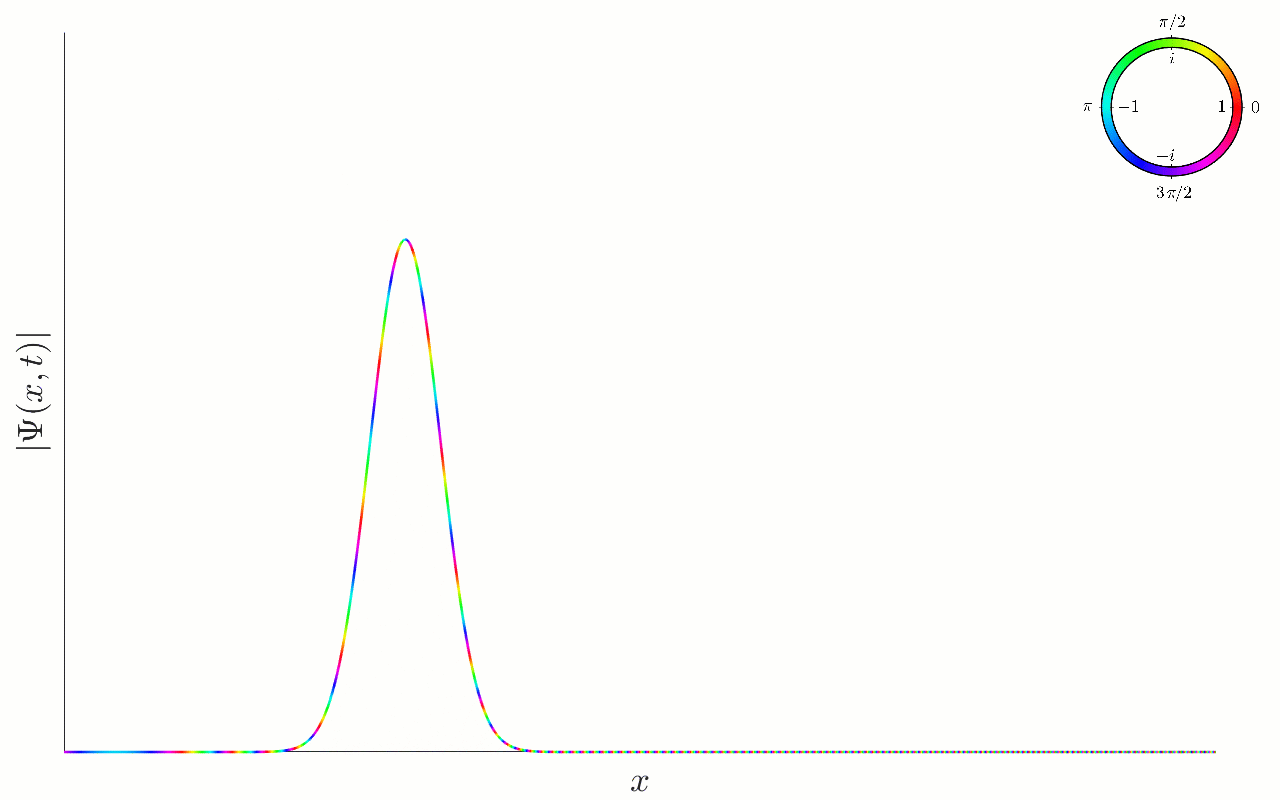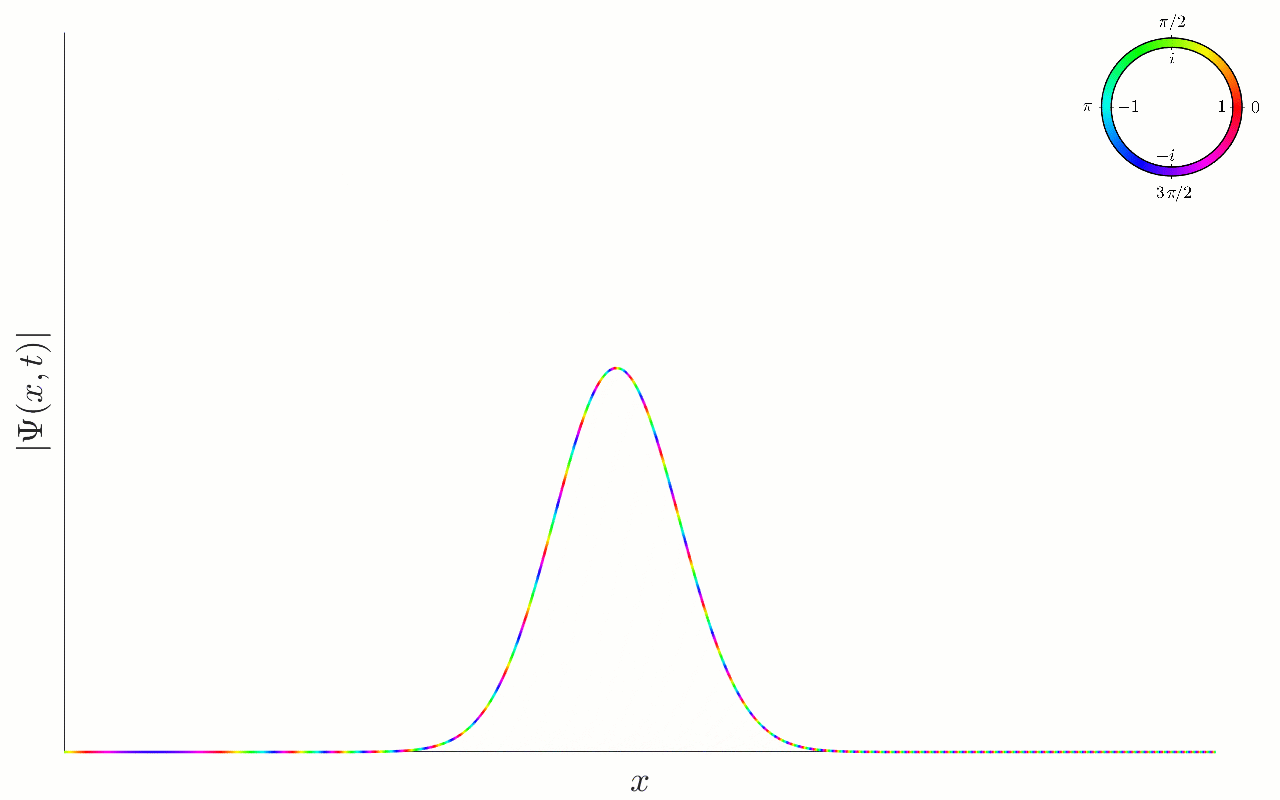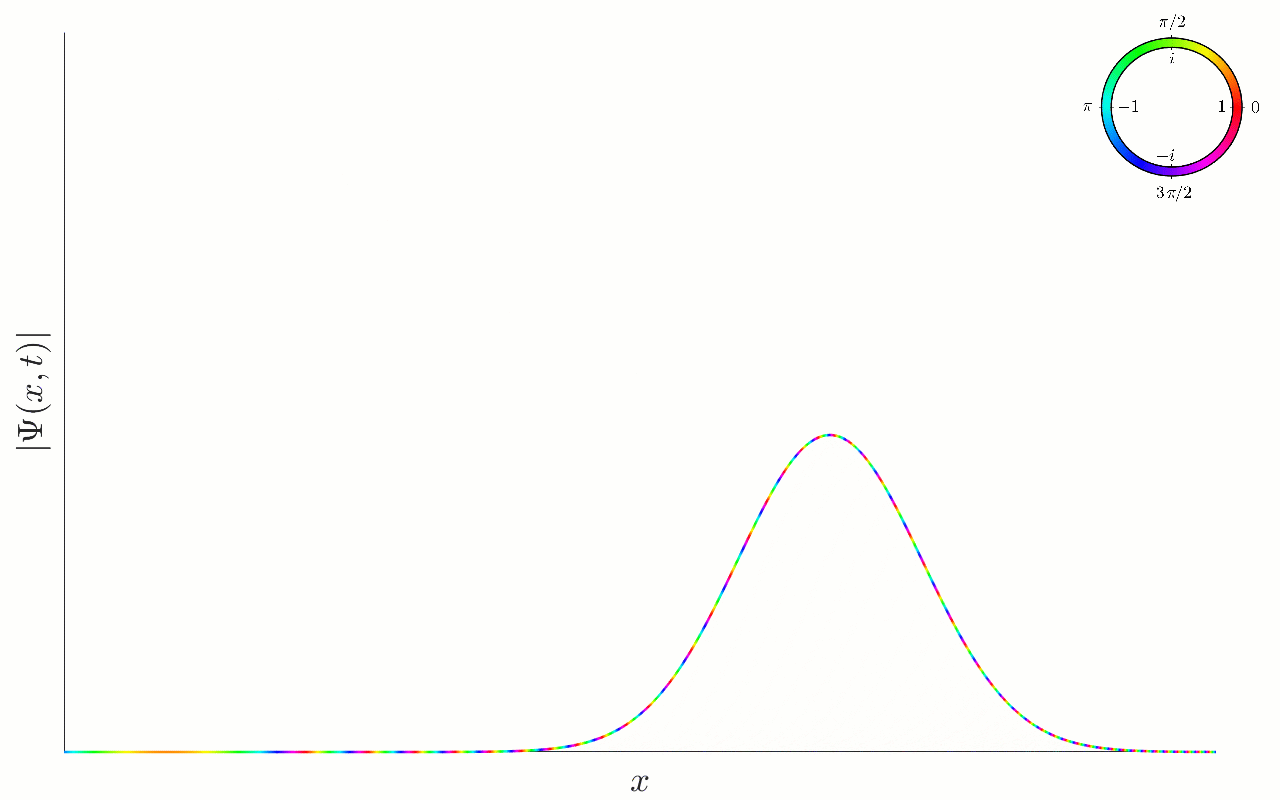
Figure 6.1:Time evolution of a gaussian wavefunction, as given in (6.12). The parameter determines the ‘width’ of the wavefunction. Here we represent the complex number at each location and time in polar form, in terms of the amplitude (the height), and phase, represented by the colour (with the colour-wheel legend at the top). The particle has a non-zero average momentum , and moves to the right at constant speed, spreading out as it moves.
Figure 6.2:Time evolution of probability density for a gaussian wavefunction as given in (6.12).
6.5Spreading of wavefunctions¶
We will end this chapter by discussing in more detail the spreading of wavefunctions of free particles in time. This is a universal feature (not just a feature of the gaussian example above), and arises due to the HUP, hence is a genuinely quantum phenomenon.
Recall from the HUP, that any initial wavefunction we consider , will necessarily have a superposition of momenta. In particular, it will have an associated momentum wavefunction , which determine which momenta the particle has. Now, if a particle would have had a definite momenta, then it would move with definite velocity. However, it has a superposition of momenta, and hence it will move with a superposition of velocities.
If we consider a fixed time, we therefore see that the particle will have a superposition of displacements. This is precisely what leads to the spreading of wavefunctions. We can see two interesting hallmarks of this if we look carefully. First, from the HUP, we know that in order for a particle to have an initial wavefunction which is more localised in space (i.e. with a smaller ), then it will necessarily need to have a larger spread of momentum . From the above discussion, we should therefore expect it to spread faster in time. This is precisely what we see analytically for the gaussian in (6.14): if we make smaller, then increases.
Second, this also explains why the phase factor occurs (and has a complicated form!). As we have explained above, the spreading is due to the superposition of momenta. It therefore follows that if the particle is further away (at the ‘front’ of the wavefunction) at later times, we would expect it to have higher momentum, and if it is closer to the initial location (at the ‘back’ of the wavefunction), we would expect it to have lower momentum. That is, correlations build up in time between where the particle is and what momentum it has. This is precisely what is captured by the phase factor, and why we should always expect to have some phase factor in time.